0. 들어가며

저번글에서는 간단한 Linear Regression에 대해서 살펴보았다. 이번에는 Logistic Regression에 대해서 간단히 살펴보자.

1. Discriminative Model의 간단한 요약 정리

1.2 Logistic Regression

독립 변수의 선형 결합을 이용하여 사건의 발생 가능성을 예측하는데 사용되는 통계 기법이다.

  • 로지스틱 회귀분석은 선형회귀랑은 다르게 결과가 범주형일때 사용되며 결과값이 기왕이면 범주형(우선은 Binary으로)으로 나와야한다. 우리가 이전에 했던 선형회귀의 경우 y의 값이 \(-\infty \sim \infty\) 인데 이진의 경우는 0과 1로 정해진다. 결국엔 문제는 우리가 가진 값의 결과와 기존 선형식의 결과의 범위가 문제가 된다.\([0, 1] \neq [-\infty, \infty]\) 이 비를 \([-\infty, \infty]=[-\infty, \infty]\)로 바꾸기 위해서 두가지 작업이 필요한데 첫번째가 Odds 비, 두번째가 log이다.

  • odds(승산)비는 실패 확률에 대한 성공 확률의 비율이다.

\[\begin{aligned} odds = \frac{P\left(A\right)}{P\left(A^{C}\right)} = \frac{P\left(A\right)}{1-P\left(A\right)} \end{aligned}\]

위의 식에서 P(A)가 1에 수렴하면 할수록 odds의 값은 무한대로 갈 것이고 P(A)가 0이라면 결과 값은 0이 될 것이다.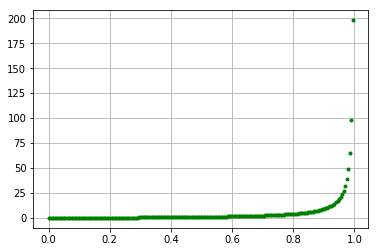gen_logit_01

  • 위의 식에서 우리는 최대값은 무한대로 변경하였지만 아직 최소값이 0으로 \(-\infty\)랑 맞지 않는다. 우리가 구한 odds비에 log 를 취하면 최소값은 \(-\infty\), 최대값은 \(\infty\) 로 우리가 구하고자하는 회귀식의 범위와 맞게 된다.

    \[\begin{aligned} \beta_{0}x_{0} + \beta_{1}x_{1}\cdots = \\ \overrightarrow{\beta}^{T}\overrightarrow{x} = &\ \ln\left(\frac{P\left(Y=1\vert X=x\right)}{1-P\left(Y=1|x=x\right)}\right) \end{aligned}\]

    라는 식이 완성된다. 이제 위 식을 우리가 익히 알고있는 Logistic Regression Model, Logistic Regression의 활성함수모양으로 변형해보자.

    \[\begin{aligned} \overrightarrow{\beta}^{T}\overrightarrow{x} = &\ \ln\left(\frac{P\left(Y=1\vert X=x\right)}{1-P\left(Y=1|x=x\right)}\right) \\ \frac{P}{1-P} =&\ e^{\beta x} \\ \frac{1-P}{P} =&\ \frac{1}{P}- 1= \frac{1}{e^{\beta x}}\\ \frac{1}{P} =&\ \frac{1}{e^{\beta x}} + 1 = \frac{1+e^{\beta x}}{e^{\beta x}} \\ P =&\ \frac{e^{\beta x}}{1 + e^{\beta x}} \\ =&\ \frac{e^{\beta x}}{1 + e^{\beta x}} \frac{\frac{1}{e^{\beta x}}}{\frac{1}{e^{beta x}}} = \frac{1}{\frac{1}{e^{beta x}}+1} \\ =&\ \frac{1}{1+e^{-\beta x}} \end{aligned}\]

    이렇게 변경된 식의 그래프는

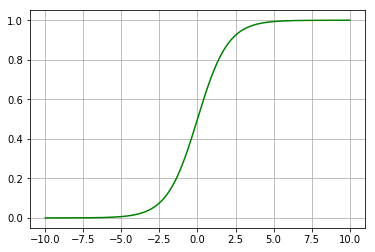
    gen_logit_02

    와 같은 S를 그리는 로지스틱 함수 혹은 시그모이드 함수라 불리는 모형을 가진다.

  • Logistic Regression의 Cost function으로는 보통 Cross Entropy를 많이 사용한다. 여러가지 이유가 있지만 일반적인 Linear Regression의 Cost function을 사용하면 Convex function 모양이 되질않는다고 한다(…). 따라서 Local minimum이 생겨서 Global minimum을 찾기 힘들어진다한다.

  • 일반적으로 사용되는 Cost function의 모양은 아래와 같다.

    \[\begin{aligned} J\left(\theta\right) = &\ \frac{1}{m}\sum cost\left(h_{\theta}\left(x\right), y\right) \\ cost\left(h_{\theta}\left(x\right),y\right) = &\ \begin{cases} -\log\left(h_{\theta}\left(x\right)\right) & \text{y = 1}\\ -\log\left(1-h_{\theta}\left(x\right)\right) & \text{y = 0} \end{cases}\\ \end{aligned}\] \[-y\log\left(h_{\theta}\left(x\right)\right)-\left(1-y\right)\log\left(1-h_{\theta}\left(x\right)\right)\]

  • Logistic Regression의 확률적 해석.

    • Hypothesis를 x가 주어졌을때 y에 대한 조건부 확률 \(P\left(Y\vert X\right)\)라 생각하자.

      \[\begin{aligned} P\left(y=1 \vert x;\theta\right) =&\ h_{\theta}\left(x\right) \\ P\left(y=0 \vert x;\theta\right) =&\ 1-h_{\theta}\left(x\right) \end{aligned}\]

    • 이는 Bernoulli distribution으로 표현이 가능하다.

\[\begin{aligned} P\left(y\vert x;\theta\right) =& \ \left(h_{\theta}\left(x\right)\right)^{y}\left(1-h_{\theta}\left(x\right)\right)^{1-y} \\ y\vert x;\theta \sim&\ \mathscr{Bernoulli}\left(\phi\right) \end{aligned}\]

  • 이러한 관측 데이터들이 독립시행으로 얻어졌다고 가정을 하고 \(\theta\)에 대한 likelihood 함수를 다음과 같이 적을 수 있다.

    \[\begin{aligned} L\left(\theta\right) = &\ P\left(\overrightarrow{y}\vert X;\theta\right) \\ = &\ \prod_{i=1}^{m}P\left(y^{i}\vert X^{i};\theta\right) \\ = &\ \prod_{i=1}^{m}\left(h_{\theta}\left(x^{\left(i\right)}\right)\right)^{y^{\left(i\right)}}\left(1-h_{\theta}\left(x^{\left(i\right)}\right)\right)^{1-y^{\left(i\right)}} \\ l\left(\theta\right) = &\ \log L\left(\theta\right) \\ = &\ \sum_{i=1}^{m}y^{\left(i\right)}\log h\left(x^{\left(i\right)}\right) + \left(1-y^{\left(i\right)}\right)\log\left(1-h\left(x^{\left(i\right)}\right)\right) \end{aligned}\]

    위와 같이 최종적으로 나온 함수의 모양이 앞에서 구한 Cross Entropy의 꼴이 된다.